산술연산의 문제점과 해결 방법
문제점
- 결과 값이 픽셀의 최댓값과 최솟값을 넘을 수 있음
해결 방법
- 클램핑 기법
음수가 나온다면 최소값을 0으로 하고 255가 넘는 값이 나온다면 최댓값을 255로 설정함
- 랩핑 기법(잘안쓰는 기법이다.)
연산의 결과 값이 최대값보다 크면 최솟값부터 최댓값까지를 한 주기로 해서 반복
최댓값+1 = 최솟값
연산의 결과 값이 최댓값 + 상수 값일 때는 계속 상수 값 -1로 설정함
ex) 결괏값: 259 => 255 + 4 => 4-1 = 3
이진수의 논리연산
논리곱(AND, ∧ ): 주어진 복수 명제 모두가 참인지
논리합(OR, ∨ ): 주어진 복수 명제에 적어도 1개 이상의 참이 있는지
배타적 논리합(XOR, ⊕ ): 주어진 2개의 명제 가운데 1개만 참일 경우를 판단
부정(NOT, ~): 명제의 참과 거짓을 반전
| A | B | A AND B | A OR B | A XOR B | NOT A | NOT B |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
AND g(x, y) = f(x, y) ∧ m(x, y)
OR g(x, y) = f(x, y) ∨ m(x,y)
XOR g(x,y) = f(x,y) ⊕ m(x,y)
NOT g(x,y) = ~ f(x,y)
픽셀 값의 AND연산
- 원하는 비트를 선택 저긍로 0으로 만드는 기능 있어 마스크(mask) 연산이라고도 함
- 영상의 특정 픽셀 비트에서 0으로 구성된 이진 데이터와 AND연산을 수행
십진수 이진수
180(10): 1011 0101(2)
0(10): 0000 0000 (2) 검정
AND연산 값: 0000 0000
64(10): 0100 0000(2)
255(10): 1111 1111(2) 흰색
AND연산 값: 0100 0000
픽셀 값의 OR연산
- 특정 비트를 선택적으로 1로 구성할 수 있어 선택적-세트(selective-set) 연산이라고도 함
- 픽셀의 특정 비트를 모두 1로 만들고자 할 때, OR 연산 수행
십진수 이진수
180(10): 1011 0101(2)
0(10): 0000 0000 (2) 검정
OR연산 값: 1011 0101
64(10): 0100 0000(2)
255(10): 1111 1111(2) 흰색
OR연산 값: 1111 1111
픽셀 값의 XOR연산
- 두 데이터를 비교하므로(compare) 연산이라고도 함
- 입력이 서로 다를 때만 1을 출력하는 연산, 같은 비트에서는 0을 출력함
십진수 이진수
180(10): 1011 0101(2)
0(10): 0000 0000 (2) 검정
XOR연산 값: 1011 0101
64(10): 0100 0000(2)
255(10): 1111 1111(2) 흰색
XOR연산 값: 1011 1111
이미지의 논리연산 예제
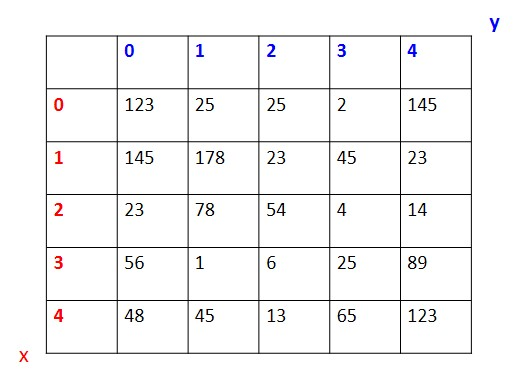
(8자리로 맞춰주기 위해서 앞을 0으로 채운다.)
- AND f(1,4) ∧ 100 = 23 ∧ 100
0001 0111
∧ 0100 0100
0000 0100 => 4(10)
- OR f(2,1) ∨ 125 = 78 ∨ 125
0110 1110
∨0111 1101
0111 1111=> 127(10)
- XOR f(0,3) ⊕ 85 = 2 ⊕ 85
0000 0010
⊕ 0101 0101
0101 0111 => 87(10)
- NOT ~ f(1,2) = ~23
0001 0111 => 1110 1000
'study > Image Information Processing' 카테고리의 다른 글
| 이미지의 히스토그램 (1) | 2023.10.30 |
|---|---|
| 다양한 포인트 처리 기법 (2) | 2023.10.16 |
| 데이터 구조 (2) | 2023.10.15 |
| 이미지 신호 (0) | 2023.09.25 |
| 신호의 디지털화 (0) | 2023.09.18 |



