Importance of Activation Functions
활성화 기능의 중요성
활성화 함수의 목적은 네트워크에 비선형성을 도입하는 것이다.
만약 우리가 녹색과 빨간색 점을 구별하기 위해 신경망을 구축하기를 원한다면 어떨까?
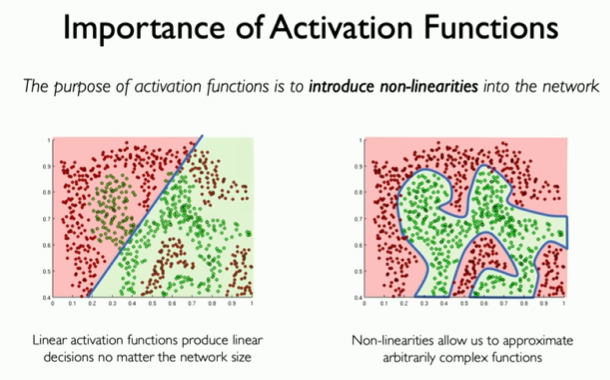
사진의 왼쪽 선형 활성화 함수는 입력 신호의 가중합은 선형 함수이고
오른쪽은 비선형성은 활성화 함수는 비선형 함수이다.
선형성은 퍼셉트론이 선형 분류기임을 의미한다.
즉, 퍼셉트론은 입력 신호의 관계를 선형적으로 학습할 수 있다.
비선형은 퍼셉트론이 복잡한 관계를 학습할 수 있도록 한다.

- 원을 뉴런 또는 노드라고 부른다.
- 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다.
- 뉴런에서 전달받은 신호의 총합이 임계값를 넘을 때만 1을 출력한다.

이미지의 좌표 부분은 퍼셉트론이 분류하는데 데이터의 좌표를 나타낸다. 좌표의 x축은 입력 신호를 x1을 나타내고, y축은 입력 신호 x2를 나타낸다. 이미지에서는 퍼셉트론이 0과 1을 분류하는 것으로 나와 있습니다. 즉, 좌표 평면에서 x1과 x2의 값이 1인 점을 0으로 분류하고, 좌표 평면에서 x1과 x2의 값이 0인 점을 1로 분류한다.
저 좌표에서 x1은 -1, x2는 2를 나타낸다.
공식에 대입을 해보자면
- 퍼셉트론 공식에 대입
y= g(1(1)+ 3(x1)- 2(x3))
y= g(1(1)+ 3(-1)- 2(2))
y= g(1-3-4)= g(-6)
구한 g(-6) 값을 시그모이드 함수로 가정하여 대입한다.
- 시그모이드 공식에 대입
g(x) = 1/ 1(1 + e^(-x)) //e는 자연 상수를 나타내며 e의 값은 2.718281828459045
이 함수는 x의 값이 증가할 수록 1에 가까워지는 함수이다. 따라서, x의 값이 -6인 경우, 시그모이드 함수의 출력은 다음과 같다.
g(-6) = 1 / (1 + e^(-(-6)))
g(-6) = 1/ (1 + e^6)
g(-6) = 1 / (1 + e^6) => 1 / (1 + 2.718281828459045 ^ 6)
값은 약 0.002
x의 값이 음수일 경우, g(x)는 0에 가까워짐
'Artificial Intelligence > Deep Leaning' 카테고리의 다른 글
| 역전파 알고리즘(Backpropagation algorithm) (6) | 2024.01.05 |
|---|---|
| Training Neural Networks(뉴럴 네트워크 훈련) (6) | 2023.12.31 |
| Applying Neural Networks(신경망 적용) (4) | 2023.12.30 |
| Building Neural Networks with Perceptrons(퍼셉트론을 이용한 신경망 구축) (6) | 2023.12.22 |
| Why Deep Learning? (딥러닝이란?) (2) | 2023.12.18 |



