1. 데이터에 대한 이해(Data Definition)
선형 회귀를 위해 사용할 예제는 공부한 시간과 점수에 대한 상관관계이다.
1시간 : 2점
2시간 : 4점
3시간 : 6점
4시간:?
ex) 위에 표를 보고 어떤 학생이 1시간 공부를 했더니 2점을 맞았다. 그렇다면, 내가 4시간을 공부한다면 몇 점을 맞을 수 있을까?
이 질문에 대답하기 위해서 앞서 나온 정보를 이용해야 한다. 이때 예측을 위해 사용하는 데이터를 훈련 데이터셋(training dataset)이라고 한다. 학습이 끝난 후, 이 모델이 얼마나 잘 작동하는지 판별하는 데이터셋을 테스트 데이터셋(test dataset)이라고 한다.
1-2. 훈련 데이터셋의 구성
앞서 텐서에 대해서 배웠는데, 모델을 학습시키기 위한 데이터는 파이토치의 텐서의 형태(torch.tensor)를 가지고 있어야 한다. 그리고 입력과 출력을 각기 다른 텐서에 저장할 필요가 있다. 이때 보편적으로 입력은 x, 출력은 y를 사용하여 표기한다.
# x_train은 공부한 시간, y_train은 그에 맵핑되는 점수를 의미한다.
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[4],[6]])
2. 가설(Hypothesis) 수립
머신 러닝에서 식을 세울 때 이 식을 가설이라고 한다. 보통 머신 러닝에서 가설은 임의로 추측해서 세워보는 식일 수도 있고, 경험적으로 알고 있는 식일 수도 있다. 그리고 맞는 가설이 아니라고 판단되면 계속 수정해나가게 되는 식이기도 하다.
선형 회귀의 가설은 이미 널리 알려져 있으므로 고민할 필요가 없다. 선형 회귀란 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 일입니다. 이때 선형 회귀의 가설(직선의 방정식)은 아래에 같은 형식을 가집니다.
y = Wx + b
가설 H를 따서 y대신 다음과 같은 식을 표현하기도 한다.
H(x) = Wx + b
이때 x와 곱해지는 W를 가중치(Weight)라고 하며, b를 편향(bias)이라고 한다.
3. 비용 함수(Cost function)에 대한 이해
*비용 함수(cost function) = *손실 함수(loss function) = 오차 함수(error function) = 목적 함수(objective function)
전부 같은 용어로 본다.(비용 함수와 손실 함수는 중요하다.)
비용 함수에 대해서 이해하기 위해서 여기서만 잠깐 새로운 예제를 사용해 보자. 어떤 4개의 훈련 데이터가 있고, 이를 2차원 그래프에 4개의 점으로 표현한 상태라고 하자

지금 목표는 4개의 점을 가장 잘 표현하는 직선을 그리는 일입니다. 임의로 3개의 직선을 그려보자

위의 그림은 서로 다른 W와 b의 값에 따라서 천자만별로 그려진 3개의 직선의 모습을 보여준다. 이 3개의 직선 중에서 4개의 점을 가장 잘 반영한 직선은 어떤 직선인가?라는 물음에 느낌적으로 검은색 직선이라고 할 수 있지만 수학에서는 의미가 없는 논리이다. 그래서 오차(error)라는 개념을 도입한다.

위 그림은 임의로 그려진 주황색 선에 대해서 각 실제값(4개의 점)과 직선의 예측값(동일한 x값에서의 직선의 y값)에 대한 값의 차이를 빨간색 화살표로 표현한 것이다. 각 실제값과 예측값과의 차이고, 이를 각 실제값에서의 오차라고 말할 수 있다. 이 직선의 예측값들과 실제값들과의 총 오차(total error)는 어떻게 구할까?
방법을 알아보자. 위 주황색 직선의 식은 y = 13x + 1이며, 각 오차는 다음과 같다.
| hours(x) | 2 | 3 | 4 | 5 |
| 실제값 | 25 | 50 | 42 | 61 |
| 예측값 | 27 | 40 | 53 | 66 |
| 오차 | -2 | 10 | -9 | -5 |
각 오차를 계산해 보자. 그런데 수식적으로 단순히 '오차 = 실제값 - 예측값'으로 정의하면 오차값이 음수가 나오는 경우가 생긴다. 이 경우, 오차를 모두 더하면 뎃셈 과정에서 오차값이 +가 되었다가 -되었다가 하므로 제대로 된 오차의 크기를 측정할 수 없다. 그래서 오차를 그냥 전부 더한 것이 아니라, 각 오차들을 제곱해 준 뒤에 전부 더해주는 것이다.

이때 데이터의 개수인 n으로 나누면, 오차의 제곱합에 대한 평균을 구할 수 있는데 이를 평균 제곱 오차(Mean Squared Error, MSE)라고 한다.

이를 실제로 계산하면 52.5가 됩니다. 이는 y = 13x + 1의 예측값과 실제값의 평균 제곱 오차의 값이 52.5 임을 의미한다.
평균 제곱 오차는 이번 회귀 문제에서 적절한 W와 b를 찾기 위해서 최적화된 식입니다. 그 이유는 평균 제곱 오차의 값을 최솟값으로 만드는 W와 b를 찾아내는 것이 가장 훈련 데이터를 잘 반영한 직선을 찾아내는 일이기 때문이다.
평균 제곱 오차를 W와 b에 의한 비용 함수(Cost function)로 재정의해보면 다음과 같다.
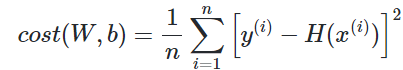
다시 정리하자면, Cost(W, b)를 최소가 되게 만드는 W와 b를 구하면 훈련 데이터를 가장 잘 나타내는 직선을 구할 수 있다.
4. 옵티마이저 - 경사 하강법(Gradient Descent)
이제 앞서 정의한 비용 함수의 값을 최소로 하는 W와 b를 찾는 방법에 대해서 배울 차례이다. 이때 사용되는 것이 옵티마이저(Optimizer) 알고리즘이다. 최적화 알고리즘이라고도 부른다. 그리고 이 옵티마이저 알고리즘을 통해 적절한 W와 b를 찾아내는 과정을 머신 러닝에서 학습(training)이라고 부른다. 여기서는 가장 기본적인 옵티마이저 알고리즘인 경사 하강법(Gradient Descent)에 대해서 배운다.
이번 설명에서 편향 b는 고려하지 않고, b가 0이라고 가정한 y=Wx와 같은 식을 기준으로 설명한다.
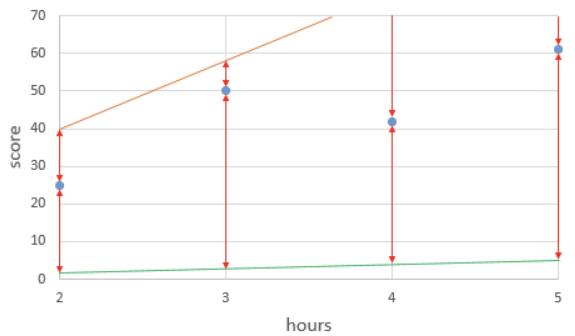
가중치 W가 직선의 방정식에서는 기울기다. 이제 W를 기울기라고 하고 설명하자면,
위의 그림에서 주황색선 기울기 W가 20일 때, 초록색선은 기울기 W가 1일 때를 보여준다. 즉, y=20x, y=x에 해당하는 직선이다. 빨간 화살표 선은 각 점에서의 실제값과 두 직선의 예측값과의 오차를 보여준다. 이는 앞서 예측에 사용했던 y= 13x + 1 직선보다 확연히 큰 오차값들이다. 즉, 기울기가 지나치게 크면 실제값과 예측값의 오차가 커지고, 기울기가 지나치게 작아도 실제값과 예측값의 오차가 커집니다. 사실 b 또한 마찬가지인데 b가 지나치게 크거나 작으면 오차가 커집니다.
편양 b가 없이 단순히 가중치 W만을 사용한 H(x) = Wx라는 가설을 가지고, 경사 하강법을 설명하자. 비용 함수의 값 cost(W)는 cost라고 줄여서 표현하고, W와 cost의 관계를 그래프로 표현하자

기울기가 W가 무한대로 커지면 커질수록 cost의 값 또한 무한대로 커지고, 반대로 기울기 W가 무한대로 작아져도 cost의 값은 무한대로 커진다. 위의 그래프에서 cost가 가장 작을 때는 맨 아래 W 축과 가장 가까운 부분이다. 기계가 해야 할 일은 cost가 가장 최솟값을 가지게 하는 W를 찾는 일이므로, 맨 아래의 볼록한 부분의 W의 값을 찾아야 한다.
기계는 임의의 초기값 W값을 정한 뒤에, 맨 아래의 볼록한 부분을 향해 점차 W의 값을 수정해 나간다. 이를 가능하게 하는 것이 바로 경사 하강법(Gradient Descent)이다.

위의 그림의 초록색 선은 W가 임의의 값을 가지게 되는 네 가지의 경우에 대해서, 그래프 상으로 접선의 기울기를 보여준다. 주목할 것은 맨 아래의 볼록한 부분으로 갈수록 접선의 기울기가 점차 작아진다는 점잉다. 그리고 맨 아래의 볼록한 부분으로 갈수록 접선의 기울기가 0이 된다.
즉, cost가 최소화가 되는 지점은 접선의 기울기가 0이 되는 지점이며, 또한 미분값이 0이 되는 지점이다. 경사 하강법의 아이디어는 비용 함수(Cost function)를 미분하여 현재 W에서의 접선의 기울기를 구하고, 접선의 기울기가 낮은 방향으로 W의 값을 변경하는 작업을 반복하는 것이다.
이 반복 작업에는 현재 W에 접선의 기울기를 구해 특정 숫자 α를 곱한 값을 빼서 새로운 W로 사용하는 식이 사용됩니다.

기울기가 음수일 때와 양수일 때 어떻게 W값이 조정되는지 보자
- 기울기가 음수일 때: W의 값이 증가

기울기가 음수면 W의 값이 증가하는데 이는 결과적으로 접선의 기울기가 0인 방향으로 W의 값이 조정된다. 만약, 접선의 기울기가 양수라면 위의 수식은 아래와 같이 표현할 수 있다.
- 기울기가 양수일 때: W의 값이 감소

기울기가 양수면 W의 값이 감소하게 되는데 이는 결과적으로 기울기가 0인 방향으로 W의 값이 조정됩니다. 즉, 아래의 수식은 접선의 기울기가 음수 거나, 양수일 때 모두 접선의 기울기가 0인 방향으로 W의 값을 조정한다.

그렇다면 여기서 학습률(learning rate)이라고 말하는 α는 어떤 의미를 가질까? 학습률 α은 W의 값을 변경할 때, 얼마나 크게 변경할지를 결정한다. 또는 W를 그래프의 한 점으로 보고 접선의 기울기가 0일 때까지 경사를 따라 내려간다는 관점에서는 얼마나 큰 폭으로 이동할지를 결정한다. 직관적으로 생각하기에 학습률 α의 값을 무작정 크게 하면 접선의 기울기가 최솟값이 되는 W를 빠르게 찾을 수 있을 것 같지만 그렇지 않다.

위의 그림은 학습률 α가 지나치게 높은 값을 가질 때, 접선의 기울기가 0이 되는 W를 찾아가는 것이 아니라 cost의 값이 발산하는 상황을 보여준다. 반대로 학습률 α가 지나치게 낮은 값을 가지면 학습 속도가 느려지므로 적당한 α의 값을 찾아낸 는 것도 중요하다.
지금까지 b는 배제시키고 최적의 W를 찾아내는 것에만 초점을 맞추어 경사 하강법의 원리에 대해 학습했다. 실제 경사 하강법은 W와 b에 대해서 동시에 경사 하강법을 수행하면서 최적의 W와 b의 값을 찾아간다.
선형 회귀에 가장 적합한 비용 함수는 평균 제곱 오차, 옵티마이저는 경사 하강법이다.
4. 파이토치로 선형 회귀 구현하기
4-1. 먼저 기본 세팅을 해줍니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim현재 실습하고 있는 파이썬 코드를 재실행해도 다음에 같은 결과가 나오도록 랜덤 시드(rand seedd)를 만들어 준다.
torch.manual_seed(1)
#<torch._C.Generator at 0x2a113441d30>실습을 위한 기본적인 세팅이 끝났다.
4-2. 변수 선언
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])x_train과 x_train의 크기를 출력해 보자
print(x_train)
print(x_train.shape)
# tensor([[1.],
# [2.],
# [3.]])
# torch.Size([3, 1])x_train의 값이 출력되고, x_train의 크기가(3x1) 임을 알 수 있다.
y_train과 y_train의 크기(shape)를 출력해 보자.
print(y_train)
print(y_train.shape)
# tensor([[2.],
# [4.],
# [6.]])
# torch.Size([3, 1])y_train의 값이 출력되고, y_train의 크기가 (3x1) 임을 알 수 있다.
4-3. 가중치와 편향의 초기화
선형 회귀란 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 일이다.
그리고 가장 잘 맞는 직선을 정의하는 것은 바로 W와 b입니다.
선형 회귀의 목표는 가장 잘 맞는 직선을 정의하는 W와 b의 값을 찾는 것이다.
우선 가중치 W를 0으로 초기화하고, 이 값을 출력해 보자.
#가중치 w를 0으로 초기회하고 학습을 통해 값이 변경되는 변수임읗 명시한다.
W = torch.zeros(1, requires_grad = True)
#가중치 W를 출력
print(W)
# tensor([0.], requires_grad=True)가중치 W가 0으로 초기화되어 있으므로 0이 출력된 것을 확인할 수 있다. 위에서 requires_grad=True가 인자로 주어진 것을 확인할 수 있다. 이는 이 변수는 학습을 통해 계속 값이 변경되는 변수임을 의미한다.
마찬가지로 편향 b도 0으로 초기화하고, 학습을 통해 값이 변경되는 변수임을 명시한다.
b = torch.zeros(1, requires_grad=True)
print(b)
# tensor([0.], requires_grad=True)현재 가중치 W와 b 둘 다 0이므로 현 직선의 방정식은 y = 0 * X + 0
지금 상태에선 x에 어떤 값이 들어가도 가설은 0을 예측하게 된다. 즉, 아직 적절한 W와 b의 값이 아니다.
4-4. 가설 세우기
파이토치 코드 상으로 직선의 방정식에 해당되는 가설을 선언한다.

hypothesis = x_train * W + b
print(hypothesis)
4-5. 비용 함수 선언하기
파이토치 코드 상으로 선형 회귀의 비용 함수에 해당하는 평균 제곱 오차를 선언한다.

#앞서 배운 torch.mean으로 평균을 구한다.
cost = torch.mean((hypothesis - y_train)** 2)
print(cost)
# tensor(18.6667, grad_fn=<MeanBackward0>)
4-6. 경사 하강법 구현하기
이제 경사 하강법을 구현한다. 아래의 'SGD'는 경사 하강법의 일종입니다. lr은 학습률(learning rate)을 의미한다. W와 b가 SGD의 입력이 됩니다.
optimizer = optim.SGD([W, b], lr=0.01)optimizer.zero_grad()를 실행하므로 미분을 통해 얻은 기울기를 0으로 초기화합니다. 기울기를 초기화해야만 새로운 가중피 편향에 대해서 새로운 기울기를 구할 수 있습니다. 그다음 cost.backward() 함수를 호출하여 가중치 W와 편향 b에 대한 기울기가 계산된다. 그다음 경사 하강법 최적화 함수 opimizer의. step() 함수를 호출하여 인수로 들어갔던 W와 b에서 리턴되는 변수들의 기울기에 학습률(learining rate) 0.01을 곱하여 빼줌으로써 업데이트합니다.
#gradient를 0으로 초기화
optimizer.zero_grad()
#비용 함수를 미분하여 gradient계산
cost.backward()
#w와 b를 업데이트
optimizer.step()requires_grad=True와 backward()에 대한 정리는 자동 미분(Autograd) 챕터에 별도 정리하였습니다.
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)
nb_epochs = 1999 # 원하는만큼 경사 하강법을 반복
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))결과적으로 훈련 과정에서 W와 b는 훈련 데이터와 잘 맞는 직선을 표현하기 위한 적절한 값으로 변환해 간다.
Epoch 0/2000 W: 0.187, b: 0.080 Cost: 18.666666
Epoch 100/2000 W: 1.746, b: 0.578 Cost: 0.048171
Epoch 200/2000 W: 1.800, b: 0.454 Cost: 0.029767
Epoch 300/2000 W: 1.843, b: 0.357 Cost: 0.018394
Epoch 400/2000 W: 1.876, b: 0.281 Cost: 0.011366
Epoch 500/2000 W: 1.903, b: 0.221 Cost: 0.007024
Epoch 600/2000 W: 1.924, b: 0.174 Cost: 0.004340
Epoch 700/2000 W: 1.940, b: 0.136 Cost: 0.002682
Epoch 800/2000 W: 1.953, b: 0.107 Cost: 0.001657
Epoch 900/2000 W: 1.963, b: 0.084 Cost: 0.001024
Epoch 1000/2000 W: 1.971, b: 0.066 Cost: 0.000633
Epoch 1100/2000 W: 1.977, b: 0.052 Cost: 0.000391
Epoch 1200/2000 W: 1.982, b: 0.041 Cost: 0.000242
Epoch 1300/2000 W: 1.986, b: 0.032 Cost: 0.000149
Epoch 1400/2000 W: 1.989, b: 0.025 Cost: 0.000092
Epoch 1500/2000 W: 1.991, b: 0.020 Cost: 0.000057
Epoch 1600/2000 W: 1.993, b: 0.016 Cost: 0.000035
Epoch 1700/2000 W: 1.995, b: 0.012 Cost: 0.000022
Epoch 1800/2000 W: 1.996, b: 0.010 Cost: 0.000013
Epoch 1900/2000 W: 1.997, b: 0.008 Cost: 0.000008
Epoch 2000/2000 W: 1.997, b: 0.006 Cost: 0.000005에포크(Epoch)는 전체 훈련 데이터가 학습에 한 번 사용된 주기를 말한다. 이번 실습의 경우 2,000번을 수행한다.
최종 훈련 결과를 보면 최적의 기울기 W는 2에 가깝고, b는 0에 가까운 것을 볼 수 있다.
현재 훈련 데이터가 x_train은 [[1], [2], [3]]이고 y_train은 [[2], [4], [6]]인 것을 감안하면 실제 정답은 W가 2이고, b가 0인 H(x) = 2x이므로 거의 정답을 찾은 셈입니다.
5. optimizer.zero_grad()가 필요한 이유
파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시키는 특징이 있습니다.
import torch
w = torch.tensor(2.0, requires_grad=True)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
z = 2*w
z.backward()
print('수식을 w로 미분한 값 : {}'.format(w.grad))수식을 w로 미분한 값: 2.0
수식을 w로 미분한 값: 4.0
수식을 w로 미분한 값: 6.0
수식을 w로 미분한 값: 8.0
수식을 w로 미분한 값: 10.0
수식을 w로 미분한 값: 12.0
수식을 w로 미분한 값: 14.0
수식을 w로 미분한 값: 16.0
수식을 w로 미분한 값: 18.0
수식을 w로 미분한 값: 20.0
수식을 w로 미분한 값: 22.0
수식을 w로 미분한 값: 24.0
수식을 w로 미분한 값: 26.0
수식을 w로 미분한 값: 28.0
수식을 w로 미분한 값: 30.0
수식을 w로 미분한 값: 32.0
수식을 w로 미분한 값: 34.0
수식을 w로 미분한 값: 36.0
수식을 w로 미분한 값: 38.0
수식을 w로 미분한 값: 40.0
수식을 w로 미분한 값: 42.0계속해서 미분값인 2가 누적되는 것을 볼 수 있다. 그렇기 때문에 optimizer.zero_grad()을 통해 미분값을 계속 0으로 초기화시켜줘야 한다.
6. torch.manual_seed()를 하는 이유
torch.manual_seed()를 사용한 프로그램의 결과는 다른 컴퓨터에서 실행시켜도 동일한 결과를 얻을 수 있다. 난수 발생 순서와 값을 동일하게 보장해 준다는 특징 때문이다.
torch.manual_seed(3)
print('랜던 시드가 3일 때')
for i in range(1,3):
print(torch.rand(1))
# 랜던 시드가 3일 때
# tensor([0.0043])
# tensor([0.1056])랜던 시드가 3일 때 두 개의 난수를 발생시켰더니 0.0043, 0.1056이 나온다. 이제 랜던 시드값을 4로 변경하고 run을 하고 다시 3으로 바꿔 준 다음에 run을 해주면 프로그램을 다시 시작하는 것처럼 난수 발생 순서가 초기화된다. 아까와 다시 동일하게 0.0043과 0.1056이 나온 것을 확인할 수 있다.
- 텐서에는 requires_grad라는 속성이 있다. 이것을 Ture로 설정하면 자동 미분 기능이 적용된다. 선형 회귀부터 신경망과 같은 복잡한 구조에서 파라미터들이 모두 이 기능이 적용된다. requires_grad = True가 적용된 텐서에 연산을 하면, 계산 그래프가 생성되며 backward 함수를 호출하면 그래프로부터 자동으로 미분이 계산된다.
- PyTorch로 시작하는 딥 러닝 입문을 참고해서 작성한 블로그 입니다.
'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| nn.Module로 구현하는 선형 회귀 (0) | 2024.03.04 |
|---|---|
| 다중 선형 회귀(Multivariable Linear regression) (10) | 2024.02.02 |
| 자동 미분(Autograd) (8) | 2024.01.26 |
| 머신 러닝 워크 플로우 (2) | 2023.12.22 |


